In combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column. Here is an example:
The name "Latin square" was inspired by mathematical papers by Leonhard Euler, who used Latin characters as symbols.[citation needed] Other symbols can be used instead of Latin letters: in the above example, the alphabetic sequence A, B, C can be replaced by the integer sequence 1, 2, 3.
[edit]Reduced form
A Latin square is said to be reduced (also, normalized or in standard form) if both its first row and its first column are in their natural order. For example, the above Latin square is not reduced because its first column is A, C, B rather than A, B, C.
We can make any Latin square reduced by permuting (reordering) the rows and columns. Here switching the above matrix's second and third rows yields
which is reduced: Both its first row and its first column are alphabetically ordered A, B, C.
[edit]Properties
[edit]Orthogonal array representation
If each entry of an n × n Latin square is written as a triple (r,c,s), where r is the row, c is the column, and s is the symbol, we obtain a set of n2 triples called the orthogonal array representation of the square. For example, the orthogonal array representation of the first Latin square displayed above is:
- { (1,1,1),(1,2,2),(1,3,3),(2,1,2),(2,2,3),(2,3,1),(3,1,3),(3,2,1),(3,3,2) },
where for example the triple (2,3,1) means that in row 2 and column 3 there is the symbol 1. The definition of a Latin square can be written in terms of orthogonal arrays:
- A Latin square is the set of all triples (r,c,s), where 1 ≤ r, c, s ≤ n, such that all ordered pairs (r,c) are distinct, all ordered pairs (r,s) are distinct, and all ordered pairs (c,s) are distinct.
For any Latin square, there are n2 triples since choosing any two uniquely determines the third. (Otherwise, an ordered pair would appear more than once in the Latin square.)
The orthogonal array representation shows that rows, columns and symbols play rather similar roles, as will be made clear below.
[edit]Equivalence classes of Latin squares
Many operations on a Latin square produce another Latin square (for example, turning it upside down).
If we permute the rows, permute the columns, and permute the names of the symbols of a Latin square, we obtain a new Latin square said to be isotopic to the first. Isotopism is an equivalence relation, so the set of all Latin squares is divided into subsets, called isotopy classes, such that two squares in the same class are isotopic and two squares in different classes are not isotopic.
Another type of operation is easiest to explain using the orthogonal array representation of the Latin square. If we systematically and consistently reorder the three items in each triple, another orthogonal array (and, thus, another Latin square) is obtained. For example, we can replace each triple (r,c,s) by (c,r,s) which corresponds to transposing the square (reflecting about its main diagonal), or we could replace each triple (r,c,s) by (c,s,r), which is a more complicated operation. Altogether there are 6 possibilities including "do nothing", giving us 6 Latin squares called the conjugates (also parastrophes) of the original square.
Finally, we can combine these two equivalence operations: two Latin squares are said to be paratopic, also main class isotopic, if one of them is isotopic to a conjugate of the other. This is again an equivalence relation, with the equivalence classes called main classes, species, or paratopy classes. Each main class contains up to 6 isotopy classes.
There is no known easily computable formula for the number L(n) of n × n Latin squares with symbols 1,2,...,n. The most accurate upper and lower bounds known for large n are far apart. One classic result is

(this given by van Lint and Wilson).
Here we will give all the known exact values. It can be seen that the numbers grow exceedingly quickly. For each n, the number of Latin squares altogether (sequence A002860 in OEIS) is n! (n-1)! times the number of reduced Latin squares (sequence A000315 in OEIS).
The numbers of Latin squares of various sizes| n | reduced Latin squares of size n | all Latin squares of size n |
| 1 | 1 | 1 |
| 2 | 1 | 2 |
| 3 | 1 | 12 |
| 4 | 4 | 576 |
| 5 | 56 | 161280 |
| 6 | 9408 | 812851200 |
| 7 | 16942080 | 61479419904000 |
| 8 | 535281401856 | 108776032459082956800 |
| 9 | 377597570964258816 | 5524751496156892842531225600 |
| 10 | 7580721483160132811489280 | 9982437658213039871725064756920320000 |
| 11 | 5363937773277371298119673540771840 | 776966836171770144107444346734230682311065600000 |
For each n, each isotopy class (sequence A040082 in OEIS) contains up to (n!)3 Latin squares (the exact number varies), while each main class (sequence A003090 in OEIS) contains either 1, 2, 3 or 6 isotopy classes.
Equivalence classes of Latin squares| n | main classes | isotopy classes |
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 1 | 1 |
| 4 | 2 | 2 |
| 5 | 2 | 2 |
| 6 | 12 | 22 |
| 7 | 147 | 564 |
| 8 | 283657 | 1676267 |
| 9 | 19270853541 | 115618721533 |
| 10 | 34817397894749939 | 208904371354363006 |
| 11 | 2036029552582883134196099 | 12216177315369229261482540 |
[edit]Examples
We give one example of a Latin square from each main class up to order 5.



They present, respectively, the multiplication tables of the following groups:












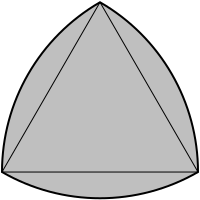

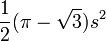 , where s is the constant width. The existence of Reuleaux polygons shows that diameter measurements alone cannot verify that an object has a circular cross-section.
, where s is the constant width. The existence of Reuleaux polygons shows that diameter measurements alone cannot verify that an object has a circular cross-section.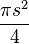 .
.



 googel
googel پنهپ
پنهپ  عکس زیبا ترین و خوشگل ترین دختر جهان
عکس زیبا ترین و خوشگل ترین دختر جهان آخرين کلمات هرکس قبل از مرگ!
آخرين کلمات هرکس قبل از مرگ! مراحله درس خوادن
مراحله درس خوادن .....................................
.....................................